Вычисление суммы - базовая математическая операция, применяемая в различных сферах. Рассмотрим основные методы и формулы для расчета сумм в разных контекстах.
Содержание
Основные математические формулы суммирования
| Тип суммы | Формула | Пример |
| Арифметическая прогрессия | S = n/2 × (a₁ + aₙ) | 1+2+3+...+100 = 5050 |
| Геометрическая прогрессия | S = a₁ × (1 - qⁿ)/(1 - q) | 1+2+4+8 = 15 |
| Сумма квадратов | S = n(n+1)(2n+1)/6 | 1²+2²+3² = 14 |
Практические методы вычисления сумм
Последовательное сложение
- Запишите все слагаемые в ряд
- Складывайте числа последовательно
- Фиксируйте промежуточные результаты
- Проверьте итоговый результат
Использование свойств сложения
- Переместительное свойство: a + b = b + a
- Сочетательное свойство: (a + b) + c = a + (b + c)
- Группировка удобных слагаемых
- Разложение на составляющие
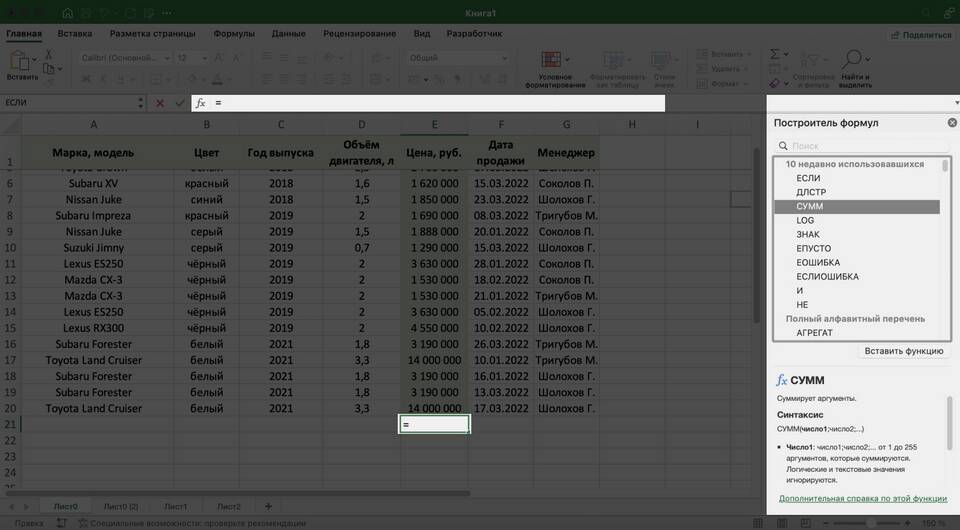
Вычисление сумм в программах
| Программа | Команда/Функция |
| Excel/Google Sheets | =SUM(A1:A10) |
| Python | sum([1, 2, 3]) |
| SQL | SELECT SUM(column) FROM table |
Вероятностные суммы
- Сумма вероятностей: P(A∪B) = P(A) + P(B) - P(A∩B)
- Полная вероятность: ΣP(Aᵢ) = 1
- Математическое ожидание суммы: E[X+Y] = E[X] + E[Y]
Финансовые расчеты сумм
- Сумма кредита с процентами: S = P(1 + r)ⁿ
- Накопленная сумма вклада: S = P(1 + r/n)ⁿᵗ
- Чистая приведенная стоимость: NPV = Σ(CFₜ/(1+i)ᵗ)
Проверка правильности вычислений
| Метод проверки | Применение |
| Обратный счет | Вычитание слагаемых из результата |
| Контрольные суммы | Использование хеш-функций |
| Статистическая оценка | Сравнение с ожидаемым диапазоном |
Особые случаи вычисления сумм
- Бесконечные ряды: Σaₙ при n→∞
- Условно сходящиеся ряды
- Знакопеременные суммы
- Кратные суммы: ΣΣaᵢⱼ
Правильное вычисление сумм требует понимания природы слагаемых и выбора оптимального метода расчета для конкретной задачи.