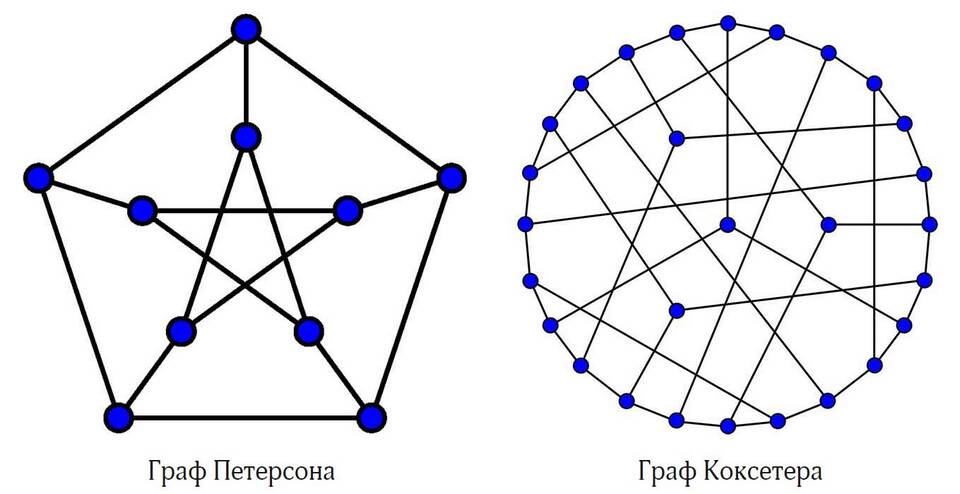
В теории графов существует фундаментальная теорема, утверждающая, что сумма степеней всех вершин графа равна удвоенному количеству его рёбер. Это утверждение известно как Лемма о рукопожатиях.
Содержание
Формулировка теоремы
Для любого неориентированного графа G = (V, E) выполняется равенство:
∑deg(v) = 2|E|
где deg(v) - степень вершины v, |E| - количество рёбер в графе.
Доказательство теоремы
- Каждое ребро графа соединяет две вершины
- При подсчёте суммы степеней каждое ребро учитывается дважды: один раз для каждой из вершин, которые оно соединяет
- Следовательно, общая сумма степеней всех вершин равна удвоенному количеству рёбер
Пример применения теоремы
| Граф | Степени вершин | Сумма степеней | Количество рёбер |
| Треугольник | 2, 2, 2 | 6 | 3 |
| Звезда с 4 лучами | 4, 1, 1, 1, 1 | 8 | 4 |
Следствия из теоремы
- В любом графе количество вершин с нечётной степенью чётно
- Средняя степень вершины в графе равна 2|E|/|V|
- В ориентированном графе сумма полустепеней исхода равна сумме полустепеней захода
Применение в теории графов
Данная теорема используется при:
- Анализе сетевых структур
- Построении алгоритмов обхода графов
- Проверке корректности описания графа
- Доказательстве других теорем теории графов